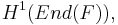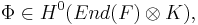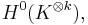Hitchin system
In mathematics, the Hitchin integrable system is an integrable system introduced by Nigel Hitchin in 1987. It lies on the crossroads of the algebraic geometry, theory of Lie algebras and integrable system theory. It also plays an important role in geometric Langlands correspondence over the field of complex numbers; related to conformal field theory as certain limit of Knizhnik–Zamolodchikov equations. Almost all integrable systems of classical mechanics can be obtained as particular systems of the Hitchin system (or its certain generalization).
Description
Using the language of algebraic geometry, the phase space of the system is the cotangent bundle to the moduli space of G-bundles for some reductive group G, on some compact algebraic curve. This space is endowed with a canonical symplectic form. Suppose for simplicity that G=GL(n), the general linear group; then the hamiltonians can be described as follows: the tangent space to G-bundles at the bundle F is
which by Serre duality is dual to
so a pair
defines a point in the cotangent bundle. Taking
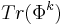 ,k=1,...,rank(G)
,k=1,...,rank(G)
one obtains elements in
which is a vector space which does not depend on 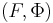 . So taking any basis in these vector spaces we obtain functions Hi, which are Hitchin's hamiltonians. The construction for general reductive group is similar and uses invariant polynomials on the Lie algebra of G.
. So taking any basis in these vector spaces we obtain functions Hi, which are Hitchin's hamiltonians. The construction for general reductive group is similar and uses invariant polynomials on the Lie algebra of G.
For trivial reasons these functions are algebraically independent, and some calculations show that their number is exactly half of the dimension of the phase space. The nontrivial part is a proof of Poisson commutativity of these functions. This is non-transparent from the algebraic geometry point of view, and one needs to go to differential geometric or Lie group viewpoints to obtain an explanation.
References
- Hitchin, Nigel (1987), "Stable bundles and integrable systems", Duke Mathematical Journal (Duke University Press) 54 (1): 91–114, doi:10.1215/S0012-7094-87-05408-1